Simplex Algorithm

The simplex algorithm implemented in OpenDa is the one due to Nelder-Mead. This is also called a Downhill Simplex Method. Simplex algorithm is one of the popular techniques in solving minimization problems, without using any derivative of the cost function to minimize. For minimization of a cost function with N parameters, it uses a polytope of (N+1) vertices. Each vertex represents a possible set of parameters, which is associated with a cost value. The minimization is performed by replacing the highest-cost vertex with a new vertex with a lower cost. The new vertex is sought for systematically by trying a sequence of different steps of moving the vertex relative to the other N vertices, until a new vertex with smaller cost is found. This procedure is repeated for the new polytope until convergence is reached, that is when the costs of all vertices are within a predefined bound of tolerance. The first trial step is simply to reflect the worst vertex with respect to the centroid of the remaining N vertices. Depending on whether the reflected cost is higher or lower than the previous ones, the algorithm will try out different step to see if it will produce a vertex with even smaller cost. In short the possible steps are reflection, expansion, contraction, and reduction. The figures below illustrate all these steps for a case of two parameters (N=2). The left most vertex is the one with highest cost. The white vertex is the newly tried vertex.

Reduction:

Contraction:
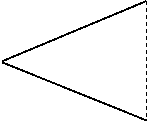
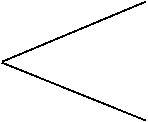